Equation Of Parabola Ellipse And Hyperbola
A hyperbola plural hyperbolas.
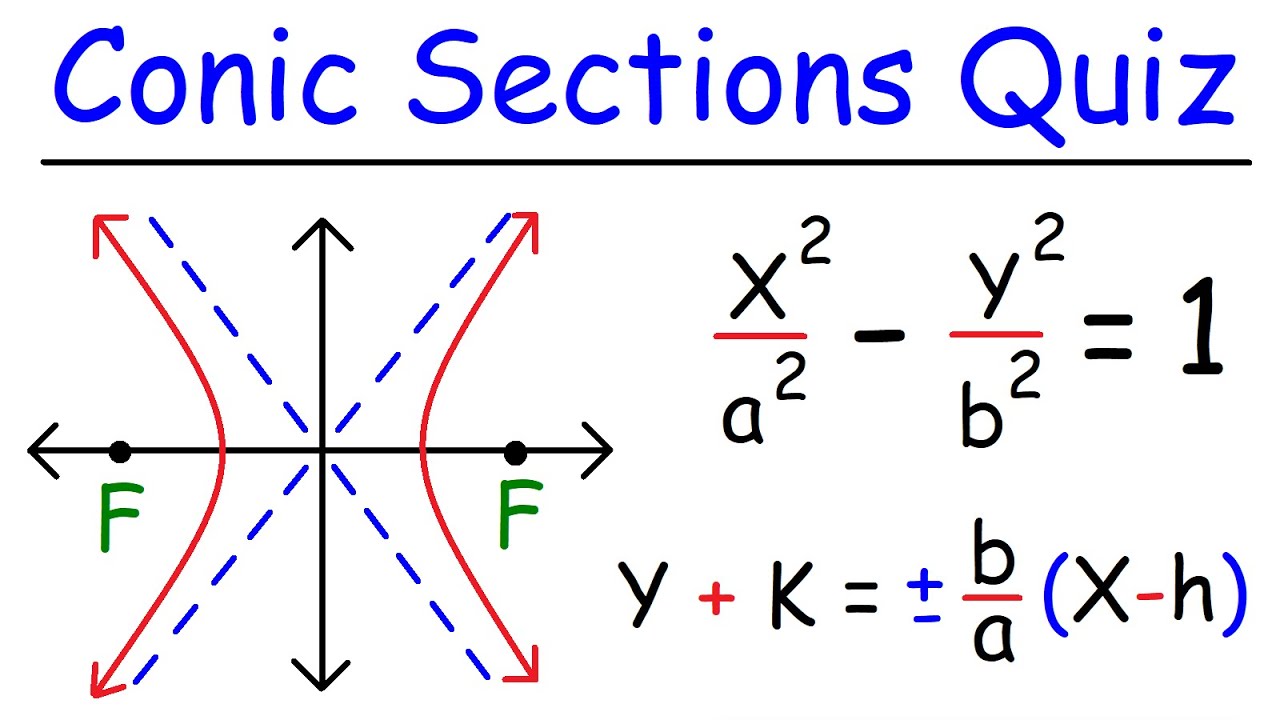
Equation of parabola ellipse and hyperbola. This is an applet to explore the equation of a parabola and its properties. The equation used is the standard equation that has the form y k 2 4ax h. In mathematics a hyperbola plural hyperbolas or hyperbolae is a type of smooth curve lying in a plane defined by its geometric properties or by equations for. Problems with detailed solutions on equation of hyperbola.
Equation of hyperbola graphing problems. Problems with detailed solutions on the hyperbola equation. Learn about the four conic sections and their equations. Circle ellipse parabola and hyperbola.
One description of a parabola involves a point the focus and a line the directrix. The focus does not lie on the directrix. The parabola is the locus of points in. A parabola is a conic section that is created when a plane cuts a conical surface parallel to the side of the cone.
A hyperbola is created when a plane cuts a conical. An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r2 from two fixed points f1 and f2 the foci separated by a.
What Is The Difference Between Identifying A Parabola Ellipse
Links Forward Conic Sections
How Do You Determine Circle Parabola Ellipse Or Hyperbola From
Conic Sections Circle Parabola Ellipse And Hyperbola Algebra
Conic Sections Circles Ellipses Parabolas Hyperbola How To
Conic Sections
Conic Sections Aerospace Engineering
Circles Ellipse Parabolas Hyperbolas Ppt Video Online Download
Conic Sections Parabolas Hyperbolas Ellipses Circles Graphing
Conic Sections
Conic Sections Circle Ellipse Hyperbola Parabola Wall Posters
Eccentricity Of Conic Sections Study Com
Definition And Examples Directrix Define Directrix Pre Calculus
Conic Sections Circle Ellipse Hyperbola Parabola Wall Posters
Conic Sections
Conic Sections Cheat Sheet Foldable For Circle Parabola Ellipse
Conic Section Wikipedia
Sparknotes Sat Subject Test Math Level 2 Other Important Graphs
Day 7 Hw Test D Part 2 Circle Parabola Ellipse Hyperbola Youtube
Elementos De Las Conicas Los Conoces Math Pinterest Math
Conics Circles Parabolas Ellipses And Hyperbolas She Loves Math
4 4 Conics Recognize The Equations And Graph The Four Basic Conics
Conic Sections And Standard Forms Of Equations
Conic Sections Circle Ellipse Hyperbola Parabola Wall Posters
Conic Section Wikipedia
Solution Find The Equation Of The Hyperbola With Vertices 4 2
Introduction To Conic Sections Parabola Hyperbola Ellipse Each
Conic Sections
Polar Equations Of Conics
Conic Sections Eccentricity Ppt Video Online Download
Introduction To Conic Sections Parabola Hyperbola Ellipse Each
Conic Sections
The Beauty Of Ellipses Parabolas And Hyperbolas Science4all
Parametric Equations Of Ellipses And Hyperbolas
Eccentricity Of Conic Sections Study Com
Conics Circles Parabolas Ellipses And Hyperbolas She Loves
The Second Degree Equations Determine Whether The Following
Conic Sections And Standard Forms Of Equations
Conic Section Wikipedia
Summary Conics Circles Parabolas Ellipses And Hyperbolas She
8 1 Conics
Parametric Equations Of Ellipses And Hyperbolas
Conic Section Wikipedia
Conics Sections Art Project
Chapter 10 Review Mth 253 Calculus Conics And Quadratic Equations
Solved Classify The Graph Of The Equation As A Circle A
Conic Section Wikipedia
Solution Find The Equation Of The Parabola Given Its Axis Vertex
Conic Sections Precalculus Math Khan Academy
Solved Identify The Type Of Conic Section Whose Equation
